Rotacional:
tienen derivadas parciales continuas en alguna región R. El rotacional
del campo F está dado por:
Para recordar mejor el vector del rotacional de F, se puede
considerar el desarrollo del siguiente determinante
Propiedades del Rotacional:
Si el campo escalar f (x,y,z) tiene derivadas parciales continuas de
segundo orden entonces el rot (∇f) = 0 .
Si el campo vectorial F (x,y,z) es una función definida sobre todo ℜ ^3 cuyas
componentes tienen derivadas parciales continuas y el rot (F) = 0
entonces F es un campo vectorial conservativo.
El rotacional de un campo vectorial tiene su principal interpretación
física cuando la función vectorial F (x,y,z) representa el flujo de un fluido,
el rotacional en este caso se interpreta como la circulación que presenta el
fluido alrededor de un punto ( x0,y0,z0)
Si el campo vectorial F representa el flujo de un fluido y rot (F) = 0
entonces se dice que el fluido es irrotacional.
Divergencia:
La divergencia de un campo vectorial mide la diferencia entre el flujo
entrante y el flujo saliente en una superficie que encierra un elemento de
volumen dV . Si el volumen elegido solamente contiene fuentes o sumideros de un
campo, entonces su divergencia es siempre distinta de cero.
La divergencia de un campo
vectorial en un punto es un campo escalar, que se define como el flujo del
campo vectorial por unidad de volumen conforme el volumen alrededor del punto tiende
a cero, para el caso del campo magnético la divergencia viene dada por la ecuación

donde S es una superficie cerrada que se reduce a un punto en el límite,
B es el campo magnético, V es el volumen que encierra dicha superficie S
y ∇es el operador nabla, que se calcula
de la sigueinte forma:

La divergencia de un campo es un valor escalar con signo. Si este signo es positivo, quiere decir que el campo emana hacia el exterior de dicho punto y, por tanto, es una fuente o manantial. Si el signo es negativo, el campo converge hacia un punto del interior del volumen, por lo que constituiría un sumidero. Si la divergencia fuese cero el campo neto (diferencia entre las líneas entrantes y salientes) sería nulo.
En el caso de los campos magnéticos se ha comprobado la ausencia de
fuentes y/o sumideros de ahí que una de sus propiedades sea que su divergencia
es nula.
Los campos cuya divergencia es cero se denominan campos solenoidales,
que se caracterizan porque sus líneas de campo son cerradas sobre si mismas, es
decir, no tienen extremos donde nacen o mueren. De tener dichos extremos, el
flujo neto alrededor de uno de ellos no sería nulo, lo cual denotaría la
existencia de una fuente o sumidero del campo.

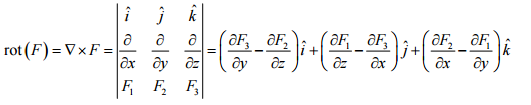
No hay comentarios:
Publicar un comentario